#include< stdio.h> < فرع />#include< stdlib.h>
fact_recursive طويل غير موقع (اسم قصير غير موقع)
{
إذا كان (الرقم == 0)
إرجاع 1 ؛
else
رقم الإرجاع * fact_recursive (رقم - 1) ؛
}
unsigned int puiss(long int x, int n)
{
if(n == 0)
return 1;
if (n == 1)
إرجاع x ؛
int x2 = power (x ، n / 2) ؛
إذا (n٪ 2 == 0)
إرجاع x2 * x2 ؛
إرجاع x2 * x2 * x ؛
}
float Approx_sin (float x ، int n)
{
جزء عائم = (عائم) puiss(x ، 2 * n-1) / (عائم) fact_recursive (2 * n-1) ؛
//display
if(n٪2==1)
printf("n = ٪d --> ٪f\n",n,fraction);
else
printf ("n = ٪d --> -٪f\n",n,fraction);
// الشرط النهائي إذا كان n = 1 ثم Approx_sin = x ؛
if (n == 1)
{
إرجاع x ؛
}
else {
// إذا كانت n فردية ، تكون العلامة موجبة
if (n٪ 2 == 1)
إرجاع calcul_formule (x ، n-1) + جزء ؛
// إذا كانت n فردية ، تكون العلامة سالبة < br / > else
إرجاع calcul_formule (x ، n-1) - كسر ؛
}
}
int main (int argc ، char * argv [])
{
int n ؛
float x ؛
printf ("أدخل قيمة x:") ؛
scanf("٪d",& x);
printf("أدخل قيمة n:");
scanf("٪d",& n);
// صيغة الحساب
printf ("Approx_sin(٪ f ، ٪ d) = ٪ f \ n" ، x ، Approx_sin (x ، n) ) ؛
النظام ("وقفة") ؛
}
Java
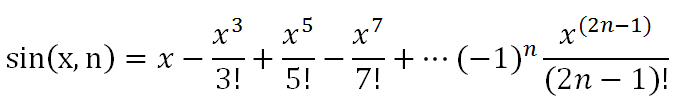
Commentaires (0)
Laisser un commentaire
Connectez-vous pour commenter
Rejoignez la discussion et partagez vos connaissances avec la communauté
Chargement des commentaires...