1- Find the GCD using the Modulo
- Assign to a the value of b and to b the value of the remainder of the division of a over b.
- Repeat until the remainder is zero.
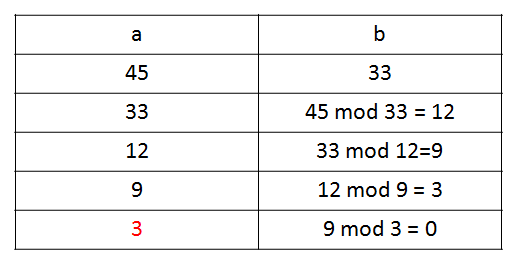
Example:
#include< stdio.h>
int main()
{
int a,b,r,x,y;
do
scanf("%d",& a);
while (a<=0);
do
scanf("%d",& b);
while (b<=0);
if (a> b)
{
x=b;
r=a%b;
}
else
{
x=a;
r=b%a;
}
while(r!=0)
{
y=x;
x=r;
r=y%x;
}
printf("%d",x);
return 0;
}
2- Find the GCD with the recursive subtractive method
If a and b are two positive integers, we have the following arithmetic properties:
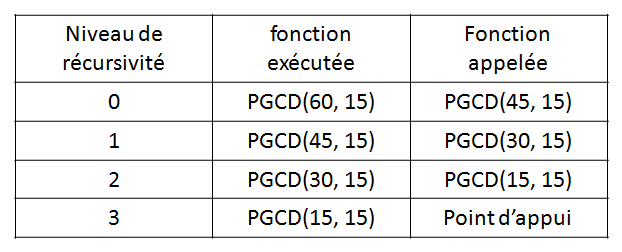
Example:
PGCD program with recursion.
int PGCD(int a, int b)
{
if(a==b)
{
return a;
}
else
{
if(a> (b)
return PGCD(a-b, b);
else
return PGCD(a, b-a);
}
}
Wikipedia: Greatest common divisor
Wikipedia: Euclid's algorithm extended
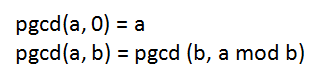
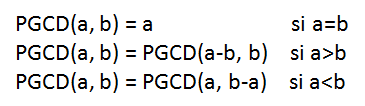
Commentaires (0)
Laisser un commentaire
Connectez-vous pour commenter
Rejoignez la discussion et partagez vos connaissances avec la communauté
Chargement des commentaires...