1- Modulo
C:#include
int main()
{
int a,b,r,x,y;
do
scanf("%d",&a);
while (a<=0);
do
scanf("%d",&b);
while (b<=0);
if (a>b)
{
x=b;
r=a%b;
}
else
{
x=a;
r=b%a;
}
while(r!=0)
{
y=x;
x=r;
r=y%x;
}
printf("%d",x);
0を返します。
}
2- 再帰減算法でGCDを見つけます
aとbが2つの正の整数の場合、次の算術プロパティがあります:
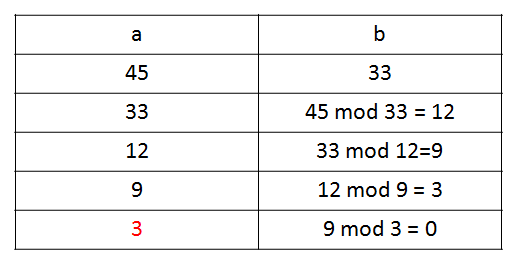
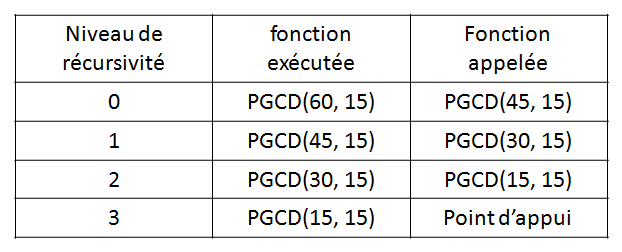
例:
PGCD プログラムと再帰。
int PGCD(int a, int b)
{
if(a==b)
{
return a;
}
else
{
if(a>(b)
return PGCD(a-b, b);
else
return PGCD(a, b-a);
}
}
Wikipedia: 最大公約数
Wikipedia: Euclid's algorithm extended
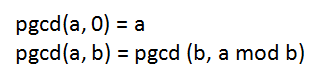
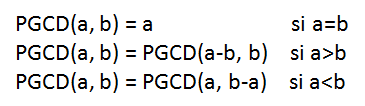
Commentaires (12)
Connectez-vous pour commenter
Rejoignez la discussion et partagez vos connaissances avec la communauté
Excellent tutoriel !
N'hésitez pas si vous avez des questions.