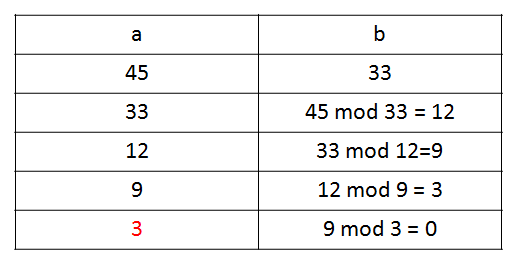
1- 모듈로를 사용하여 GCD를 찾습니다
C:#include< stdio.h>
int main()
{
int a,b,r,x,y;
do
scanf("%d",& a);
동안 (a<=0);
do
scanf("%d",& b);
동안 (b<=0);
if (a> b)
{
x=b;
r=a%b;
}
else
{
x=a;
r=b%a;
}
while(r!=0)
{
y=x;
x=r;
r=y%x;
}
printf("%d",x);
0을 반환합니다.
}
2- 재귀 뺄셈 방법으로 GCD 찾기
a와 b가 두 개의 양의 정수이면 다음과 같은 산술 속성이 있습니다.
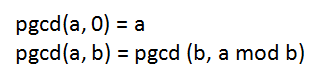
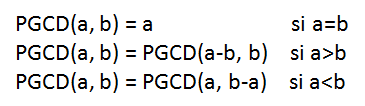 < / a>< / div>
< / a>< / div>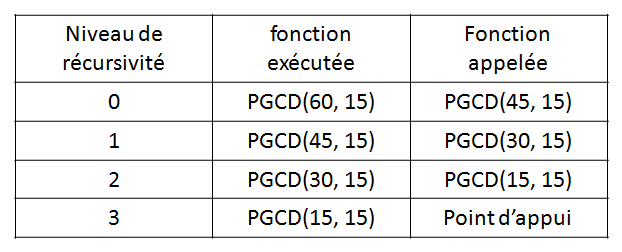
Commentaires (12)
Connectez-vous pour commenter
Rejoignez la discussion et partagez vos connaissances avec la communauté
Excellent tutoriel !
N'hésitez pas si vous avez des questions.