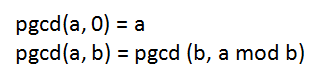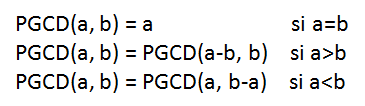Рекурсивное вычисление PGCD на языке Си
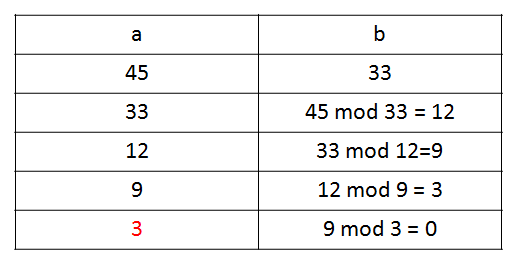
GCD (наибольший общий делитель) двух целых чисел, когда хотя бы одно из них не равно нулю, является наибольшим положительным целым делителем, делящим два числа. Например, НОД 45 и 30 равен 15.1- Найдите НОД по модулю
- Присвойте a значение b и b значение остатка от деления a на b.
- Повторяйте до тех пор, пока остаток не станет равным нулю.
Example:
#include< stdio.h>
int main()
{
int a,b,r,x,y;
do
scanf("%d",& a);
while (a<=0);
do
scanf("%d",& b);
while (b<=0);
если (a> б)
{
x=b;
r=a%b;
}
else
{
x=a;
r=b%a;
}
while(r!=0)
{
y=x;
x=r;
r=y%x;
}
printf("%d",x);
возвращаем 0;
}
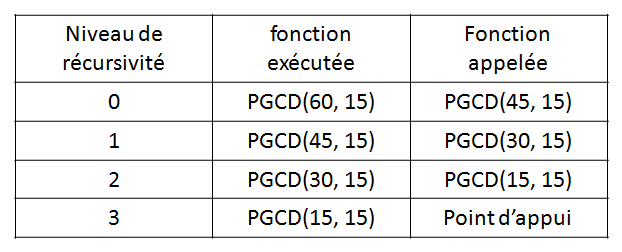
2- Найти НОД рекурсивным методом вычитания
Если a и b — два натуральных числа, то мы имеем следующие арифметические свойства:
Пример:
PGCD программа с рекурсией.
int PGCD(int a, int b)
{
if(a==b)
{
return a;
}
else
{
if(a> (b)
возврат PGCD(a-b, b);
else
return PGCD(a, b-a);
}
}
Википедия: Наибольший общий делитель
Википедия: Расширенный алгоритм Евклида