#include< stdio.h>
#include< stdlib.h>
unsigned long fact_recursive (unsigned short nombre)
{
if (number == 0)
return 1;
else
return number * fact_recursive(number - 1);
}
unsigned int puiss(long int x, int n)
{
if(n == 0)
return 1;
if(n == 1)
return x;
int x2 = power(x,n/2);
if(n%2 == 0)
return x2 * x2;
return x2 * x2 * x;
}
float Approx_sin(float x, int n)
{
float fraction = (float)puiss(x,2*n-1) / (float)fact_recursive(2*n-1);
//Display
if(n%2==1)
printf("n = %d --> %f\n",n,fraction);
else
printf("n = %d --> -%f\n",n,fraction);
//Terminal condition if n=1 then Approx_sin=x;
if(n==1)
{
return x;
}
else{
//if n is odd the sign is positive
if(n%2==1)
return calcul_formule(x, n-1)+fraction;
//if n is odd, the sign is negative
else
return calcul_formule(x,n-1)-fraction;
}
}
int main(int argc, char *argv[])
{
int n;
float x;
printf("Enter the value of x: ");
scanf("%d",& x);
printf("Enter the value of n: ");
scanf("%d",& n);
//formula calculation
printf("Approx_sin(%f, %d ) = %f\n",x,Approx_sin(x,n) );
system("pause");
}
Java
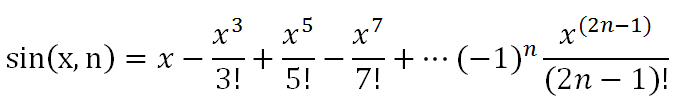
Commentaires (0)
Laisser un commentaire
Connectez-vous pour commenter
Rejoignez la discussion et partagez vos connaissances avec la communauté
Chargement des commentaires...